the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Subseasonal midlatitude prediction skill following Quasi-Biennial Oscillation and Madden–Julian Oscillation activity
Kirsten J. Mayer
Elizabeth A. Barnes
The Madden–Julian Oscillation (MJO) is known to force extratropical weather days to weeks following an MJO event through excitation of stationary Rossby waves, also referred to as tropical–extratropical teleconnections. Prior research has demonstrated that this tropically forced midlatitude response leads to increased prediction skill on subseasonal to seasonal (S2S) timescales. Furthermore, the Quasi-Biennial Oscillation (QBO) has been shown to possibly alter these teleconnections through modulation of the MJO itself and the atmospheric basic state upon which the Rossby waves propagate. This implies that the MJO–QBO relationship may affect midlatitude circulation prediction skill on S2S timescales. In this study, we quantify midlatitude circulation sensitivity and prediction skill following active MJOs and QBOs across the Northern Hemisphere on S2S timescales through an examination of the 500 hPa geopotential height field. First, a comparison of the spatial distribution of Northern Hemisphere sensitivity to the MJO during different QBO phases is performed for European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-Interim reanalysis and ECMWF and the National Centers for Environmental Prediction (NCEP) hindcasts. Secondly, differences in prediction skill in ECMWF and NCEP hindcasts are quantified following MJO–QBO activity. In both hindcast systems, we find that regions across the Pacific, North America, and the Atlantic demonstrate an enhanced MJO impact on prediction skill during strong QBO periods with lead times of 1–4 weeks compared to MJO events during neutral QBO periods.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(7419 KB)
- Corrigendum
-
Supplement
(9019 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(7419 KB) - Corrigendum
-
Supplement
(9019 KB) - BibTeX
- EndNote
Previous research has focused on the impact of the Madden–Julian Oscillation (MJO) on the extratropical circulation in order to extend midlatitude prediction skill (e.g., Henderson et al., 2016; Baggett et al., 2017; Tseng et al., 2018; Zheng et al., 2018). The MJO is a 20–90 d tropical intraseasonal convective oscillation (Madden and Julian, 1971, 1972, 1994), and through its convective heating it initiates an extratropical response through the excitation of quasi-stationary Rossby waves. These waves modulate the midlatitude circulation days to weeks following MJO activity and have been shown to provide coherent and consistent modulation of midlatitude circulation into subseasonal to seasonal (2–5 weeks; S2S hereafter) timescales (e.g., Hoskins and Karoly, 1981; Sardeshmukh and Hoskins, 1988; Henderson et al., 2016; Tseng et al., 2018).
More recent research has demonstrated a dependence of the MJO on a stratospheric phenomenon known as the Quasi-Biennial Oscillation (QBO). The QBO is an approximately 28-month, downward-propagating, zonal mean, zonal wind oscillation in the tropical stratosphere and has many subsequent impacts such as modulation of the upper tropical troposphere (e.g., Collimore et al., 2003; Garfinkel and Hartmann, 2011b; Son et al., 2017), the subtropical jet (e.g., Simpson et al., 2009; Garfinkel and Hartmann, 2011a), and the stratospheric polar vortex (e.g., Holton and Tan, 1980; Garfinkel et al., 2018). The QBO is typically divided into two phases, easterly and westerly (EQBO and WQBO, respectively), determined by the direction of the anomalous zonal wind in the lower tropical stratosphere (Baldwin and Dunkerton, 2001). Recent work has shown that the MJO convective envelope tends to be stronger and have slower eastward propagation and longer path lengths during EQBO compared to WQBO (Son et al., 2017; Nishimoto and Yoden, 2017; Densmore et al., 2019; Zhang and Zhang, 2018). Son et al. (2017) hypothesize that this slower MJO propagation during EQBO is a consequence of strengthened MJO convection, as stronger MJO events tend to propagate more slowly across the Maritime Continent. However, Zhang and Zhang (2018) argue that stronger MJO wintertime events during EQBO are a consequence of a greater number of MJO days instead of larger amplitudes of individual MJO events. While there are still uncertainties regarding the exact impacts of the QBO on the MJO, these studies demonstrate the importance of considering the QBO in MJO research.
Much of the recent MJO–QBO research has focused on the direct impacts of the QBO on the tropical tropopause, and thus MJO activity, while only a handful of studies have examined how the QBO subsequently impacts MJO teleconnections (e.g., Baggett et al., 2017; Mundhenk et al., 2018; Wang et al., 2018). Baggett et al. (2017) and Mundhenk et al. (2018) emphasize the impact of the QBO on MJO teleconnections through its modulation of MJO-induced Rossby waves and consequently changes in the steering and frequency of atmospheric rivers. Wang et al. (2018) found that when accounting for the phase of the QBO, the amplitude of the North Pacific storm track shift in response to MJO activity is greater during EQBO compared to WQBO, which they hypothesize to be from increased MJO strength during EQBO.
An MJO–QBO relationship has also been found in dynamical models. For example, Abhik and Hendon (2019) recently demonstrated that hindcast simulations, initialized with observations during active MJOs, capture the increase in MJO amplitude and maintenance during EQBO events after about 5 d. In addition, this strengthened MJO amplitude during EQBO has been shown to translate to increased MJO prediction skill (Marshall et al., 2017; Lim et al., 2019), suggesting that the prediction skill of the subsequent midlatitude teleconnections may also increase following the MJO under EQBO conditions. Baggett et al. (2017) further show that prediction skill of atmospheric rivers on timescales of 1–2 weeks varies with QBO phase within ECMWF hindcasts over North America following MJO activity. This highlights the potential for an MJO–QBO relationship to modulate midlatitude prediction skill on S2S timescales.
Since hindcast models capture the increase in MJO amplitude during EQBO as well as exhibit enhanced prediction skill of the MJO in weeks 1–3 under strong QBOs, this raises the question as to whether the MJO–QBO relationship also translates to enhanced prediction skill of MJO teleconnections under specific QBO phases. This paper explores this question through an analysis of the influence of the QBO on midlatitude prediction skill following active MJOs on S2S timescales within the ECMWF and NCEP hindcasts.
2.1 Data
We utilize daily mean 500 hPa geopotential height (z500; years 1979–2017) from the European Centre for Medium-Range Weather Forecasts (ECMWF) Interim reanalysis (ERA-I; Dee et al., 2011) as well as the ECMWF and NCEP hindcasts obtained from the S2S database established by the World Weather Research Program/World Climate Research Program (WWRP/WCRP; Vitart, 2017). The ECMWF hindcasts are composed of 11 ensemble members with hindcasts initialized four times a week (years 1995–2016). The NCEP hindcasts are composed of four ensemble members with hindcasts initialized daily (years 1999–2010). In the following analysis, the ensemble mean for both models was used, and so the different number of members between ECMWF and NCEP may contribute to differences in results between models.
We focus on December, January, and February (DJF) since MJO teleconnections are strongest during boreal winter (e.g., Madden, 1986), and the relationship between the MJO and QBO is strongest during these months as well (e.g., Yoo and Son, 2016; Son et al., 2017). The annual cycle is removed from the ERA-I reanalysis by subtracting the daily climatology of z500 across 1979–2017 from the z500 field. For the hindcast models, a daily, lead-dependent climatology is subtracted from each model's z500 field. To do this, we calculate the daily climatology for each lead time independently. Since the ECMWF model is not initialized daily, two (forward- and backward-moving) 31 d running means are applied to the climatology at all lead times to reduce noise, following Sun et al. (2018). These smoothed lead-dependent daily climatologies are then subtracted from the z500 field of the corresponding model to remove the annual cycle.
There is presently no definitive understanding of the impact of the El Niño–Southern Oscillation (ENSO) on the QBO–MJO relationship. Some earlier research indicates that ENSO has a limited impact on the QBO–MJO interaction (e.g., Yoo and Son, 2016; Nishimoto and Yoden, 2017); however, recent work on QBO–MJO teleconnections has shown a possible dependency of results on ENSO (Son et al., 2017; Wang et al., 2018; Sun et al., 2019). In addition, other research suggests that the QBO affects ENSO teleconnections (Garfinkel and Hartmann, 2010; Richter et al., 2015; Hansen et al., 2016), which may consequently impact the MJO and its teleconnections. Thus, in an attempt to ensure our results are not somehow biased by ENSO, we use the Nino3.4 Index (https://climatedataguide.ucar.edu/climate-data; Trenberth and National Center for Atmospheric Research Staff, 2020; Trenberth, 1997) to remove strong ENSO winter seasons from our analysis. Specifically, when the amplitude of the NINO3.4 index for a month within DJF is greater than 1 ∘C (signifying El Niño) or less than −1 ∘C (signifying La Niña), that DJF season is excluded from the analysis. With that said, we have repeated our analysis with ENSO seasons included and find that our STRIPES conclusions remain the same. The prediction skill conclusions also remain the same during EQBO, but WQBO results appear more sensitive to ENSO (see Supplement Figs. S6–S9). The impact of ENSO on the MJO–QBO relationship and their teleconnections still remains an active area of research.
2.2 MJO and QBO indices
The real-time multivariate MJO (RMM) index is used to define the amplitude and phase of the MJO in the ERA-I reanalysis (Wheeler and Hendon, 2004). This index uses empirical orthogonal function (EOF) analysis applied to anomalous outgoing longwave radiation (OLR) and 200 and 850 hPa zonal wind, near-equatorially averaged (15∘ S to 15∘ N), to determine the first two principal components (RMM1 and RMM2). A day is considered to have an active MJO when the RMM amplitude for that day (defined as ) is greater than 1.0. The MJO phase is then defined as tan and largely corresponds to the longitudinal location of the convective envelope. Active MJO dates within ERA-I that correspond to initialization dates in ECMWF and NCEP are determined from this index. The RMM index is not separately calculated for each hindcast model because we do not aim to quantify the ability of the models to forecast the MJO directly (e.g., Vitart, 2017). Rather, we use the index calculated from reanalysis to see how the hindcast models initialized on observed active MJO days ultimately forecast MJO teleconnections.
Identical to the definition of Yoo and Son (2016), the QBO index is calculated within ERA-I using monthly standardized zonal wind at 50 hPa, area-averaged between 10∘ S and 10∘ N. Westerly QBO (WQBO) and easterly QBO (EQBO) events are defined as when the standardized value is greater than 0.5σ or less than −0.5σ, respectively. Absolute values less than 0.5σ are considered neutral QBO (NQBO) events.
2.3 Methods
Quantification of each model's ability to represent MJO teleconnections under different QBO phases is conducted using the Sensitivities To the Remote Influence of Periodic EventS (STRIPES) index (Jenney et al., 2019). STRIPES is an index recently developed to determine regions of extratropical sensitivity to remote periodic events such as the MJO. As used here, the STRIPES index quantifies the strength and consistency of MJO teleconnections in z500 through average phase and 0–28 d lead information at individual grid points for a variety of observed phase speeds (5–8 d per phase; Wheeler and Hendon, 2004). Specifically, a composite of average z500 anomalies for each MJO phase and lead (phase–lead diagram) is created for each grid point in the Northern Hemisphere (example shown in Fig. 1a). For further intuition of the phase–lead diagram, Fig. 1b and c show composite z500 anomalies for the domain around 45∘ N and 5∘ W (marked by the white X) 12 d following phase 6 and phase 2, respectively. The value of the box in the phase–lead diagram is the same as the value plotted at the X in Fig. 1b, c. In a phase–lead diagram, MJO-induced quasi-stationary Rossby waves are apparent as slowly alternating-sign z500 anomalies with lead following a specific phase of the MJO (e.g., Fig. 1a). In addition, the MJO is a propagating phenomenon with a phase speed of approximately 5–8 d per phase. Therefore, if there is a teleconnection signal 10 d following phase 2, this signal is likely also present 5 d following phase 3 in the same region, in a composite sense. On a phase–lead diagram, this is seen as a diagonal line or “stripe” slanted at the phase speed of the MJO (Fig. 1a). Therefore, if a region is sensitive to the MJO, we expect alternating z500 anomaly stripes approximately sloped at the average phase speed of the MJO, as in Fig. 1a, which we refer to as the “stripiness”.
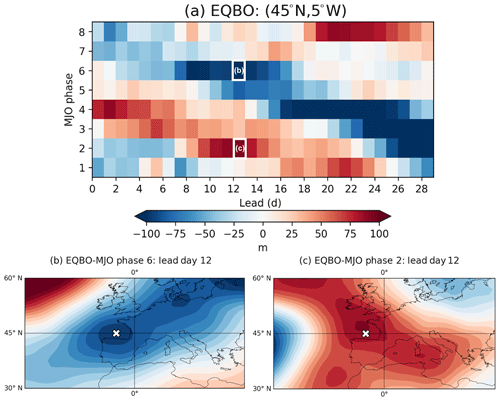
Figure 1Boreal winter (DJF) composite ERA-I z500 anomalies subsampled to ECMWF initialization dates (1995–2016) for (a) each MJO phase during EQBO vs. lead at 45∘ N and 5∘ W. White boxes and text denote the corresponding panels below. Panels (b) and (c) include composite ERA-I z500 anomalies subsampled to ECMWF initialization dates (DJF, 1995–2016) over Europe for (b) phase 6 and (c) phase 2 at lead day 12. The white X denotes 45∘ N and 5∘ W.
To calculate STRIPES, averages along the slopes in the phase–lead diagram corresponding to the MJO phase speed are calculated, and if there are alternating stripes (i.e., sensitivity to the MJO), the resulting averages concatenated together will oscillate between positive and negative z500 anomalies as a sine wave, for which the amplitude can be calculated. The amplitude of this oscillatory vector is the STRIPES index (Jenney et al., 2019). The more sensitive the region is to MJO teleconnections, the larger the STRIPES index. Therefore, the STRIPES index allows us to regionally quantify the strength, consistency, and propagation of the MJO impact on the extratropics and thus allows us to quantify the ability of hindcast models to capture tropical–extratropical teleconnections on 1- to 4-week timescales in a single metric.
For equal comparison of STRIPES between the models and reanalysis, we calculate STRIPES for ERA-I only with dates that overlap with the hindcasts; thus, the ERA-I STRIPES figures differ for ECMWF versus NCEP dates. It should be noted that the westerly phase of the QBO has been documented to reduce the propagation speed of the MJO (Nishimoto and Yoden, 2017). However, we find that our STRIPES results are robust to changes in phase speed of ±2 d per phase. Also note that since our application focuses on extratropical sensitivity in z500, we use z500 anomalies in terms of meters instead of standard deviation for STRIPES, different from Jenney et al. (2019). Standardization may mute the extratropical signal due to the greater variability of z500 in the midlatitudes, which is of the most interest here. In addition, we wish to retain any differences in z500 anomaly amplitudes between the QBO phases.
STRIPES values that are statistically larger than expected by chance are determined using a bootstrapping method. The number of random days grabbed corresponds to the observed number of days for the QBO–MJO event of interest. In order to retain autocorrelation within MJO events, we keep the day of year (DOY) and phase distribution information for each MJO event and randomly sample years (with replacement). Since the ECMWF hindcast data are not initialized on the same day each year, if the DOY needed is not available for a particular year, we instead use the date of initialization closest to this DOY. From this sample, we calculate STRIPES. This is repeated 250 times for each latitude and longitude. Any STRIPES value greater than the 90th percentile of these bootstrapped values is deemed significant. When the data are subdivided by QBO phase, we begin to see the effects of sample size on the uncertainty, leading to fewer points of significance. However, when the QBO phase is not considered or, in other words, when all MJO events are included (see Fig. S1), the statistical analysis shows significance in regions of large STRIPES values. This bootstrapping analysis is only conducted on ERA-I, as these are the “observed” sensitivities and thus the regions of interest.
To quantify midlatitude prediction skill, a daily area-weighted Pearson correlation is conducted between hindcast and ERA-I anomalous z500 (anomaly correlation coefficient, ACC). The data are separated into NQBO–, EQBO– and WQBO–MJO events in each hindcast dataset, and the corresponding reanalysis data are obtained from ERA-I. The ACC between a given model day and the same day in ERA-I is calculated within a centered 60∘ wide longitude box extending from 30 to 60∘ N. Our conclusions are not affected by the latitudinal extent of the box when it is varied by ±10–30∘ N. This calculation is repeated for every initialization and subsequent lead time as well as every 5∘ longitude beginning at 0∘ E. ACCs are grouped and averaged by QBO phase to obtain average ACCs across the Northern Hemisphere at every lead for each QBO phase (see Fig. S3 for an example).
Statistically significant differences in ACCs across lead and longitude are also computed with a bootstrapping method. Specifically, all model data within DJF are shuffled and random dates are grabbed. The number of random dates corresponds to the number of observed dates for the particular QBO phase and MJO activity being tested. These dates are then found in ERA-I. The spatial correlations between the model and the observations are calculated and then averaged to get an average ACC. This is repeated for each QBO–MJO combination, and the differences between their ACCs are calculated. The above analysis is repeated 10 000 times for each longitude and lead time. Differences greater than the 90th percentile of the 10 000 bootstrapped differences are considered significantly greater from that expected by chance. In this bootstrapping analysis, we were able to repeat the calculations 10 000 times (instead of 250) because the calculation was less computationally expensive.
3.1 Extratropical sensitivity
Figure 2a, c, and e show the STRIPES analysis of ERA-I for days within the ECMWF hindcasts, split by QBO phase. Darker shading indicates regions of greater sensitivity to the MJO for each QBO state. Regions along the North Pacific and Atlantic storm tracks as well as over North America are highlighted by STRIPES following the MJO for all phases of the QBO (Fig. 2a, c, e). This is consistent with previous research as these regions have been shown to be sensitive to MJO-excited Rossby waves through, for example, their modulation of the North Atlantic Oscillation (Cassou, 2008), the Pacific North American Oscillation (Mori and Watanabe, 2008), and Northern Hemisphere wintertime blocking (Henderson et al., 2016). Interestingly, the Pacific and Atlantic sectors have similar STRIPES values. One may expect higher STRIPES values over the Pacific compared to the Atlantic since the Pacific is generally known to have a strong response to the MJO. We hypothesize that the Atlantic and European sectors also have similar STRIPES values to those of the Pacific due to enhanced blocking over the Atlantic and Europe at later leads following the MJO (Henderson et al., 2016). Since the STRIPES index accounts for all leads as well as the strength and consistency of the z500 anomalies, we therefore expect STRIPES values over the Atlantic and European sectors to be large as well.
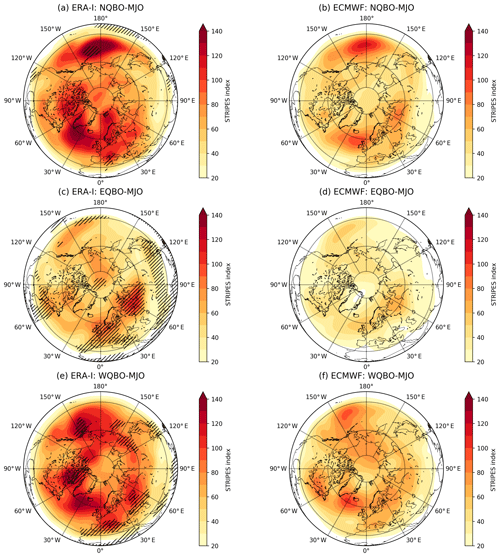
Figure 2STRIPES values for (a, c, e) ERA-Interim and (b, d, f) ECMWF for all (a, b) NQBO–MJO, (c, d) EQBO–MJO, and (e, f) WQBO–MJO events. (a, c, e) Black hatching denotes STRIPES values that are statistically larger than expected by chance at 90 % confidence in ERA-I. Significance is only calculated for ERA-I.
Figure 2b, d, and f show the STRIPES analysis of the ECMWF hindcasts for the same dates. ECMWF largely captures the spatial patterns and locations sensitive to the MJO under different QBO phases (spatial correlation with ERA-I: , , and ), but overall the model has smaller STRIPES values than ERA-I. This is likely a result of model forecast degradation at later lead times since the calculation of STRIPES utilizes z500 forecasts out to 28 d lead time.
An examination of the NCEP hindcasts shows that it also generally captures regions sensitive to the MJO under varying phases of the QBO (Fig. 3b, d, f; spatial correlation with ERA-I: , , and ) and is also weaker than the corresponding ERA-I analysis (Fig. 3a, c, e). The ERA-I STRIPES analysis for NCEP hindcasts largely has the same features as the ERA-I analysis for ECMWF hindcasts, but with larger values due to differences in sample size and dates of initialization between NCEP and ECMWF. From this STRIPES comparison (Figs. 2 and 3), we conclude that the ECMWF and NCEP hindcast models generally capture Northern Hemisphere regions sensitive to the MJO as highlighted by large spatial correlations between each model and ERA-I.
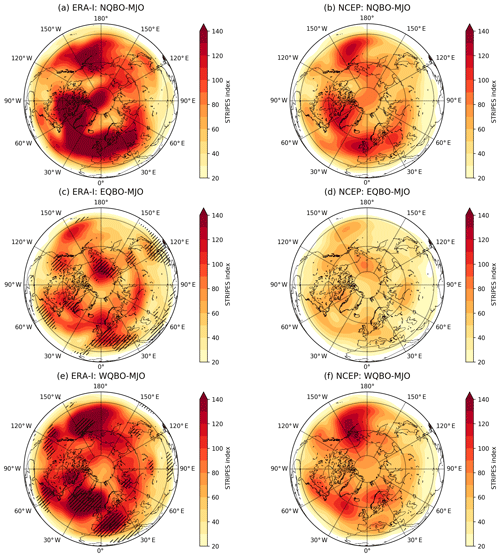
Figure 3STRIPES values for (a, c, e) ERA-Interim and (b, d, f) NCEP for all (a, b) NQBO–MJO, (c, d) EQBO–MJO, and (e, f) WQBO–MJO events. (a, c, e) Black hatching denotes STRIPES values that are statistically larger than expected by chance at 90 % confidence in ERA-I. Significance is only calculated for ERA-I.
Recent research has shown that during EQBO, the MJO amplitude is larger and the convective envelope propagates more slowly compared to MJO activity during WQBO (Son et al., 2017; Nishimoto and Yoden, 2017; Zhang and Zhang, 2018). If direct impacts on the MJO (e.g., through changes in upper tropospheric tropical static stability) lead to changes in MJO teleconnection sensitivity across the Northern Hemisphere, we might expect EQBO–MJO events to have larger midlatitude sensitivity to the MJO compared to WQBO–MJO. Instead, we find that Northern Hemisphere sensitivity to the MJO is significantly reduced during EQBO–MJO events compared to WQBO–MJO events (compare Figs. 2c, e and 3c, e; significance of difference not shown). We explored this further and found that this difference can largely be explained by the tendency of WQBO to have larger magnitude z500 anomalies compared to EQBO, not more distinct stripes. This is likely due to the larger sample size during EQBO (Table S1 in the Supplement) leading to reduced noise in the average. Therefore, when the amplitude differences between the z500 anomalies are accounted for through normalization, the difference in Northern Hemispheric sensitivity to the MJO between QBO phases is greatly reduced (Fig. S3).
3.2 Prediction skill
3.2.1 Regional prediction skill
Knowing that the ECMWF and NCEP hindcasts generally capture regional sensitivity to the MJO, we next address whether strong QBOs enhance MJO impacts on midlatitude skill. As mentioned in the introduction, EQBO has been found to impact the MJO in ways that may enhance MJO teleconnections (e.g., Son et al., 2017; Nishimoto and Yoden, 2017). Since enhanced activity may provide a prominent signal above model noise and uncertainty, and thus hypothetically lead to enhanced prediction skill, we focus here on only improved prediction skill (see Fig. S4 for regions of decreased prediction skill). Note that prediction skill at 1-week lead times is not likely to be significantly different following active MJOs compared to inactive MJOs since forecast models already have relatively good prediction skill for these early leads. Where we would expect the MJO to provide additional prediction skill is on timescales longer than 1 week. Here, skill is calculated as an anomaly spatial correlation coefficient (ACC) between z500 from the hindcasts and ERA-I (see Sect. 2.3), and we compare this skill over QBO–MJO combinations to skill during inactive MJOs. Figure 4 shows z500 ACC as a function of lead time for the North Pacific (30–60∘ N, 165∘ W), North Atlantic (30–60∘ N, 30∘ W), and Europe (30–60∘ N, 0∘ E).
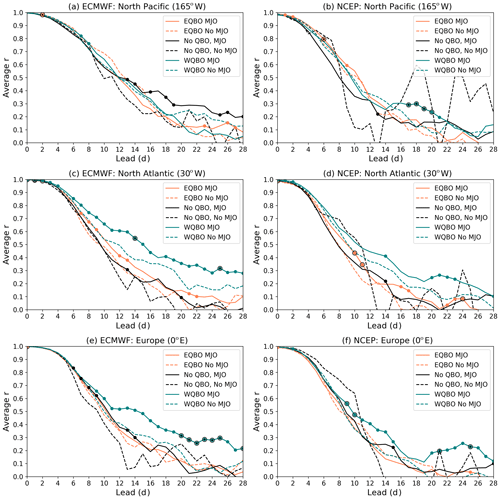
Figure 4Anomalous spatial correlation coefficient at (a, b) 165∘ W, (c, d) 30∘ W, and (e, f) 0∘ E for (a, c, e) ECMWF and (b, d, f) NCEP. Solid lines correspond to active MJOs while dashed lines correspond to inactive MJOs. Colors refer to the phase of the QBO. Colored dots denote regions and leads where requirement one is passed at 90 % confidence for the corresponding QBO. Black circles indicate regions and leads where requirement two is passed at 90 % confidence, and small black dots on orange and teal lines indicate regions and leads where requirement three is passed at 90 % confidence. See the text for details.
We invoke two requirements to address the question of whether a particular strong QBO (EQBO or WQBO) enhances the MJO impact on midlatitude prediction skill compared to an inactive QBO (NQBO) and a third requirement to answer whether the MJO leads to enhanced midlatitude prediction skill under a strong QBO compared to an NQBO. Each requirement builds on the previous requirement. For example, we can only examine requirement two if requirement one has been passed. These requirements are summarized below:
-
a significant MJO impact,
-
a significant MJO impact during a strong QBO that is significantly greater than an MJO impact during NQBO,
-
enhanced prediction skill following an MJO during a strong QBO that is significantly greater than that during NQBO.
The first requirement is the presence of an MJO impact on midlatitude prediction skill during specific phases of the QBO. An “MJO impact” on midlatitude prediction skill is defined as a significant difference in midlatitude ACC between active MJO and inactive MJO events and is denoted by colored dots in Fig. 4, in other words, where the solid line (EQBO–, WQBO–, and NQBO–MJO) is significantly above the corresponding colored dashed line (EQBO–, WQBO–, and NQBO–noMJO).
Where there is an MJO impact we continue to the second requirement. The second requirement is that the magnitude of the significant MJO impact under strong QBOs is larger than the significant MJO impact under NQBOs. This second requirement is denoted by black circles around the colored dots in Fig. 4. These two requirements together ensure that (1) there is an MJO impact and (2) this impact is enhanced during strong QBOs compared to neutral QBOs.
Requirement three specifies significantly enhanced prediction skill following an MJO during strong QBOs compared to NQBO. In Fig. 4, this is when a colored line (EQBO– and WQBO–MJO) is significantly above the black line (NQBO–MJO) and is denoted as a small black dot on a teal or orange dot. We applied this requirement to ensure that regions with enhanced MJO impacts during strong QBOs also have overall greater prediction skill following active MJO events compared to NQBO–MJO events.
For requirement one, we see that there is an MJO impact in the North Atlantic and Europe during WQBO out to week 4 in ECMWF (Fig. 4c, e; teal dots). In NCEP during WQBO, we see an MJO impact on weeks 2 and 4 over Europe and weeks 3–4 in the North Pacific and North Atlantic (Fig. 4b, d, f; teal dots). For requirement two, there is an enhanced MJO impact during WQBO in ECMWF over Europe during weeks 3–4 and in NCEP over the North Pacific in week 3. For all of the regions where requirement two is passed, requirement three is also satisfied. Therefore, where WQBO enhances the MJO impact on midlatitude prediction skill, WQBO also leads to increased prediction skill following MJO events compared to NQBO. While Fig. 4 shows results for three specific regions, we extend these results to all longitudes in Fig. 5. Specifically, the four panels show the difference in ACC between EQBO–MJO and EQBO–noMJO (Fig. 5a, b; orange solid and dashed lines in Fig. 4) and WQBO–MJO and WQBO–noMJO (Fig. 5c, d; teal solid and dashed lines in Fig. 4). Figure 5a and c show the differences within ECMWF, and Fig. 5b and d show differences within NCEP. Shading specifies increased prediction skill following the MJO compared to inactive MJOs during the specific phase of the QBO, and grey dots denote a significant MJO impact (requirement one), as denoted in Fig. 4 by the colored dots. Regions where the MJO impact is significantly enhanced during a strong QBO compared to NQBO are denoted with a black circle around the grey dots (requirement two). When the MJO leads to enhanced prediction skill during strong QBOs compared to NQBO (requirement three), a small black dot is plotted, as in Fig. 4.
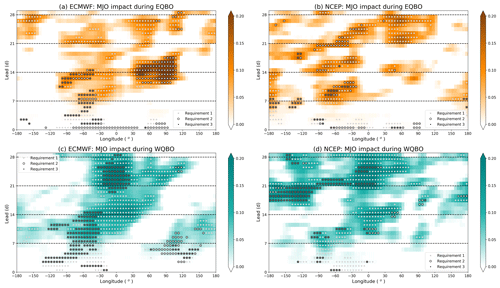
Figure 5Anomalous correlation coefficient between the (a, b) EQBO–MJO and EQBO–noMJO and (c, d) WQBO–MJO and WQBO–noMJO for (a, c) ECMWF and (b, d) NCEP at each longitude and lead from model initialization. Correlations are calculated within a 60∘ wide box, centered on each longitude, extending from 30 to 60∘ N. Shading denotes the phase of the QBO. Grey dots denote regions and leads where requirement one is passed at 90 % confidence. Black circles indicate regions and leads where requirement two is passed at 90 % confidence, and small black dots indicate regions and leads where requirement three is passed at 90 % confidence. See the text for details.
Focusing on the first requirement (grey dots), during EQBO (Fig. 5a, b), there is an MJO impact on midlatitude prediction skill in North America at week 2 leads for NCEP and ECMWF and extending into Asia, at weeks 2–3 leads for ECMWF, and at week 4 leads for NCEP. During WQBO in ECMWF and NCEP (Fig. 5c, d), there is an MJO impact in the east Pacific into North America through week 1. This impact continues through week 2 into the North Atlantic and Europe and continues over Europe for weeks 3–4 (Fig. 5c, d). In NCEP, the MJO impact also occurs in the Pacific during week 3 (Fig. 5d). From Fig. 5, we see that in both models, there is an MJO impact on midlatitude prediction skill during EQBO from North America to East Asia and during WQBO from the North Pacific through Europe on subseasonal timescales.
For the second requirement (black circles), we see that during EQBO in ECMWF (Fig. 5a) the MJO impact is greater than during NQBO over North America and the North Atlantic on weeks 1–2 and over Asia on weeks 2–3. For NCEP (Fig. 5b), this occurs over the North Pacific to the Atlantic on timescales of 1–2 weeks and again over the Atlantic in weeks 3–4. During WQBO in ECMWF (Fig. 5c), there is an enhanced MJO impact in the east Pacific into the North Atlantic through week 2. This enhanced MJO impact reemerges over the North Atlantic by week 4. In NCEP (Fig. 5d), there is an enhanced MJO impact over the Pacific on week 3 and over North America and the Atlantic on week 4. Thus, Fig. 5 suggests that strong QBOs enhance the MJO impact on midlatitude subseasonal prediction skill from the Pacific to Europe, although we remind the reader once again of the small NQBO sample sizes.
For the third requirement (small black dots), during EQBO this requirement is satisfied over North America and the North Atlantic on timescales of 1–2 weeks in ECMWF and NCEP. For WQBO in ECMWF, this requirement is satisfied over the east Pacific through the Atlantic for weeks 1–2 leads and reemerges over the North Atlantic and Europe during week 4. For NCEP, during WQBO the third requirement is satisfied on the timescale of 3–4 weeks over the North Pacific to the Atlantic. Interestingly, for WQBO in both models, the third requirement is almost always satisfied over the regions and leads where requirement two is satisfied. This suggests that WQBOs enhance the MJO impact on midlatitude prediction skill as well as enhance overall prediction skill compared to NQBOs following active MJOs from the Pacific to Europe on the timescale of 1–4 weeks in ECMWF and on the timescale of 3–4 weeks in NCEP.
Since EQBO is thought to increase the amplitude of the MJO as well as help to propagate the MJO further into the Pacific Ocean compared to WQBO (Son et al., 2017; Nishimoto and Yoden, 2017; Zhang and Zhang, 2018), one may have expected that active MJOs during EQBO conditions would lead to stronger MJO teleconnections and thus act to enhance subseasonal prediction skill in the midlatitudes. However, from Fig. 5 we see that while EQBO has an enhanced MJO impact on weeks 1–4 leads from North America to East Asia, WQBO has an enhanced MJO impact as well as enhanced overall prediction skill compared to NQBO on subseasonal timescales, specifically from the North Pacific through Europe. Perhaps most striking is the enhanced MJO impact and increased prediction skill following active MJO events during WQBO over the North Atlantic in weeks 3–4 in both ECMWF and NCEP. This result is supported by recent research showing that the North Atlantic Oscillation and MJO connection is stronger during WQBO (Feng and Lin, 2019; Song and Wu, 2020). Furthermore, enhanced prediction skill of atmospheric rivers over Alaska is also found following active MJOs during WQBO (Baggett et al., 2017). Previous research has shown that WQBO alone leads to enhanced midlatitude prediction skill over the North Atlantic (Boer and Hamilton, 2008); however, we specifically look at the difference between active and inactive MJOs under WQBO and therefore have removed any possible WQBO background skill. We also extended this analysis beyond week 4 (not shown). We find that while there is still an MJO impact through 40 d, this MJO impact is seldom significantly larger than the MJO impact during NQBOs. This suggests that strong QBOs do not lead to an enhanced MJO impact beyond 4 weeks in these models.
It should be noted that inactive MJOs during NQBO events with ENSO removed only occur 12 times in ECMWF and three times in NCEP. When this is the case, there is shading across all longitudes (Fig. S5). If ENSO events are not removed, the sample sizes increase to 47 and 52 for ECMWF and NCEP, respectively (see Table S1). When we calculate the MJO impact during NQBO when ENSO is included (Fig. S6), we see that much of the shading east of 0∘ is not apparent. The presence of skill east of 0∘ when ENSO is not included may be due to small sample sizes of the NQBO events. Thus, when comparing MJO impacts between strong and neutral QBOs, it is important to keep sample size in mind. That being said, the statistical analysis we have applied here for requirements one, two, and three account for the small sample sizes in the analysis.
The MJO is the dominant mode of intraseasonal variability in the tropics (Madden and Julian, 1971; Adames and Kim, 2016), and through its convective heating it modulates midlatitude weather, days to weeks after an MJO event (e.g., Vecchi, 2004; Zhou et al., 2012; Henderson et al., 2016; Tseng et al., 2019). Recent research has shown that the QBO impacts MJO amplitude, propagation, and prediction skill (Son et al., 2017; Nishimoto and Yoden, 2017; Zhang and Zhang, 2018; Marshall et al., 2017; Lim et al., 2019) as well as modulates MJO teleconnections (e.g., Baggett et al., 2017; Mundhenk et al., 2018; Wang et al., 2018). This raises the question as to whether the QBO also affects the prediction skill of MJO teleconnections. The goal of this study is to address this question through an examination of differences in the prediction skill in weeks 1–4 between different combinations of QBO–MJO activity.
Through a STRIPES analysis (Jenney et al., 2019), we show that ECMWF and NCEP hindcasts are capable of simulating composite midlatitude MJO sensitivity out to week 4 under different phases of the QBO. We then use these hindcasts to study enhanced S2S prediction skill following QBO–MJO activity. Increased prediction skill is determined from significant increases in spatial correlations of z500 for various QBO–MJO combinations. First, comparing active MJOs to inactive MJOs during different QBO phases (requirement one), we find that there is an MJO impact on midlatitude prediction skill during EQBO from North America to East Asia and during WQBO from the North Pacific through Europe. Second, when comparing the MJO impact between strong QBOs and NQBO (requirement two), we see that strong QBOs enhance the MJO impact on midlatitude subseasonal prediction skill from the Pacific to Europe. Lastly, to ensure that regions with enhanced MJO impacts during strong QBOs also have overall greater prediction skill following active MJO events compared to NQBO–MJO events (requirement three), we find that WQBOs enhance the MJO impact on midlatitude prediction skill as well as enhance overall prediction skill compared to NQBOs from the Pacific to Europe on the timescale of 1–4 weeks in ECMWF and 3–4 weeks in NCEP.
This study provides insight into improved prediction skill following different MJO–QBO combinations; however, more research is needed to determine the causal link between the MJO–QBO, midlatitude teleconnections, and prediction skill. It is unclear whether enhanced midlatitude prediction skill is a consequence of the QBO's direct effects on the tropical environment in which the MJO forms and/or through the modulation of the atmospheric basic state through which Rossby waves propagate.
We motivated this study by suggesting that enhanced MJO prediction following EQBO (Marshall et al., 2017; Lim et al., 2019; Abhik and Hendon, 2019) may also lead to enhanced midlatitude prediction skill following MJOs during EQBO. However, we find that both EQBO and WQBO lead to an enhanced MJO impact in these hindcasts rather than only EQBO. Enhanced skill following MJOs during both EQBO and WQBO may partially be explained by Kim et al. (2019), who find no significant impact of the QBO on MJO prediction skill within the Subseasonal Experiment database (SubX; Pegion et al., 2019), which suggests these models do not differentiate between the two phases of the QBO. In addition, we find that there is an enhanced MJO impact as well as increased prediction skill following MJO events during WQBO compared to NQBO on S2S timescales, specifically over the North Atlantic out to week 4 lead times. This result is supported by a growing body of work suggesting the importance of WQBO on MJO teleconnections. For example, recent work has shown that the North Atlantic Oscillation and MJO relationship are stronger during WQBO (Feng and Lin, 2019; Song and Wu, 2020), and prediction skill of atmospheric rivers over Alaska is enhanced following WQBO–MJO (Baggett et al., 2017). Finally, while strong ENSO events were removed from our analysis in an attempt to separate the effects of the QBO from those of ENSO, an ENSO influence may still remain. In addition, the sample sizes for MJO–QBO activity are not large (Table S1), although we attempt to account for this through statistical analysis. Even so, this work suggests that both phases of the QBO may impact prediction skill of MJO teleconnections and should be considered in future studies.
ERA-I reanalysis data are provided by the European Centre for Medium-Range Forecasts (https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim; Dee et al., 2011). The ECMWF and NCEP hindcasts are provided by the World Weather Research Program/World Climate Research Program (ECMWF: https://apps.ecmwf.int/datasets/data/s2s/levtype=sfc/type=cf/; Vitart et al., 2017 and NCEP: http://iridl.ldeo.columbia.edu/SOURCES/.Models/.SubX/; Kirtman et al., 2017). RMM Index data are provided by the Australian Bureau of Meteorology (http://www.bom.gov.au/climate/mjo/graphics/rmm.74toRealtime.txt; Wheeler and Hendon, 2004). The Nino3.4 Index data were provided by NOAA/OAR/ESRL Boulder, CO (https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni; Trenberth and National Center for Atmospheric Research Staff, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/wcd-1-247-2020-supplement.
KJM led the collection of the data, the data analysis, and writing of the manuscript. EAB aided with the experimental design, analysis techniques, and writing of the manuscript.
The authors declare that they have no conflict of interest.
This research was partially funded by NOAA research through supporting Kirsten J. Mayer and partially funded by the NOAA MAPP S2S Prediction Task Force through supporting Elizabeth A. Barnes with NOAA grant NA16OAR4310064. We also thank the reviewers for their helpful comments. In addition, we acknowledge the SubX system, specifically the climate modeling groups (Environmental Canada NASA NOAA/NCEP NRL and the University of Miami) for the model output, as well as NOAA/MAPP ONR, NASA, and NOAA/NWS for providing coordinating support and leading development of the SubX system.
This research has been supported by the NOAA research and the NOAA MAPP S2S Prediction Task Force (grant no. NA16OAR4310064).
This paper was edited by Michael Riemer and reviewed by two anonymous referees.
Abhik, S. and Hendon, H. H.: Influence of the QBO on the MJO during coupled model multiweek forecasts, Geophys. Res. Lett., 46, 9213–9221, https://doi.org/10.1029/2019GL083152, 2019. a, b
Adames, Á. F. and Kim, D.: The MJO as a Dispersive, Convectively Coupled Moisture Wave: Theory and Observations, J. Atmos. Sci., 73, 913–941, 2016. a
Baggett, C. F., Barnes, E. A., Maloney, E. D., and Mundhenk, B. D.: Advancing atmospheric river forecasts into subseasonal-to-seasonal time scales, Geophys. Res. Lett., 44, 7528—7536, https://doi.org/10.1002/2017GL074434, 2017. a, b, c, d, e, f, g
Baldwin, M. P. and Dunkerton, T. J.: Stratospheric harbingers of anomalous weather regimes, Science, 294, 581–584, 2001. a
Boer, G. J. and Hamilton, K.: QBO influence on extratropical predictive skill, Clim. Dynam., 31, 987–1000, 2008. a
Cassou, C.: Intraseasonal interaction between the Madden-Julian Oscillation and the North Atlantic Oscillation, Nature, 455, 523–527, 2008. a
Collimore, C. C., Martin, D. W., Hitchman, M. H., Huesmann, A., and Waliser, D. E.: On The Relationship between the QBO and Tropical Deep Convection, J. Climate, 16, 2552–2568, 2003. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, D. P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge‐Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011 (data available at: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim, last access: 24 April 2020). a, b
Densmore, C. R., Sanabia, E. R., and Barrett, B. S.: QBO Influence on MJO Amplitude over the Maritime Continent: Physical Mechanisms and Seasonality, Mon. Weather Rev., 147, 389–406, 2019. a
Feng, P. and Lin, H.: Modulation of the MJO-Related Teleconnections by the QBO, J. Geophys. Res.-Atmos., 124, https://doi.org/10.1029/2019JD030878, 2019. a, b
Garfinkel, C. I. and Hartmann, D. L.: The Influence of the Quasi-Biennial Oscillation on the North Pacific and El-Nino teleconnections, J. Geophys. Res.-Atmos., 115, D20116, https://doi.org/10.1029/2010JD014181, 2010. a
Garfinkel, C. I. and Hartmann, D. L.: The Influence of the Quasi-Biennial Oscillation on the Troposphere in Winter in a Hierarchy of Models. Part I: Simplified Dry GCMs, J. Atmos. Sci., 68, 1273–1289, 2011a. a
Garfinkel, C. I. and Hartmann, D. L.: The Influence of the Quasi-Biennial Oscillation on the Troposphere in Winter in a Hierarchy of Models. Part II: Perpetual Winter WACCM Runs, J. Atmos. Sci., 68, 2026–2041, 2011b. a
Garfinkel, C. I., Schwartz, C., Domeisen, D. I. V., Son, S.-W., Butler, A. H., and White, I. P.: Extratropical Atmospheric Predictability From the Quasi-Biennial Oscillation in Subseasonal Forecast Models, J. Geophys. Res.-Atmos., 123, 7855–7866, https://doi.org/10.1029/2018JD028724, 2018. a
Hansen, F., Matthes, K., and Wahl, S.: Tropospheric QBO–ENSO Interactions and Differences between the Atlantic and Pacific, J. Climate, 29, 1353–1368, 2016. a
Henderson, S. A., Maloney, E. D., and Barnes, E. A.: The Influence of the Madden–Julian Oscillation on Northern Hemisphere Winter Blocking, J. Climate, 29, 4597–4616, 2016. a, b, c, d, e
Holton, J. R. and Tan, H.-C.: The Influence of the Equatorial Quasi-Biennial Oscillation on the Global Circulation at 50 mb, J. Atmos. Sci., 37, 2200–2208, 1980. a
Hoskins, B. J. and Karoly, D. J.: The Steady Linear Response of a Spherical Atmosphere to Thermal and Orographic Forcing, J. Atmos. Sci., 38, 1179–1196, 1981. a
Jenney, A. M., Randall, D. A., and Barnes, E. A.: Quantifying Regional Sensitivities to Periodic Events: Application to the MJO, J. Geophys. Res.-Atmos., 124, 3671–3683, 2019. a, b, c, d
Kim, H., Richter, J. H., and Martin, Z.: Insignificant QBO-MJO prediction skill relationship in the subseasonal reforecasts, J. Geophys. Res.-Atmos., 124, 12655–12666, https://doi.org/10.1029/2019JD031416, 2019. a
Kirtman, B. P., Pegion, K., DelSole, T., Tippett, M., Robertson, A. W., Bell, M., Burgman, R., Lin, H., Gottschalck, J., Collins, D. C., Li, W., Sinsky, E., Guan, H., Zhu, Y., Becker, E. J., Lajoie, E., MacRitchie, K., Min, D., Fu, R., Achuthavarier, D., Koster, R., Marshak, L., Lin, H., Denis, B., Barton, N., Metzger, E. J., Sun, S., Benjamin, S., and Green, B. W.: The Subseasonal Experiment (SubX), IRI Data Library, https://doi.org/10.7916/D8PG249H, 2017. a
Lim, Y., Son, S.-W., Marshall, A. G., Hendon, H. H., and Seo, K.-H.: Influence of the QBO on MJO prediction skill in the subseasonal-to-seasonal prediction models, Clim. Dynam., 53, 1681–1695, 2019. a, b, c
Madden, R. A.: Seasonal variations of the 40–50 day oscillation in the tropics, J. Atmos. Sci., 43, 3138–3158, 1986. a
Madden, R. A. and Julian, P. R.: Detection of a 40–50 Day Oscillation in the Zonal Wind in the Tropical Pacific, J. Atmos. Sci., 28, 702–708, 1971. a, b
Madden, R. A. and Julian, P. R.: Description of Global-Scale Circulation Cells in the Tropics with a 40–50 Day Period, J. Atmos. Sci., 29, 1109–1123, 1972. a
Madden, R. A. and Julian, P. R.: Observations of the 40–50-Day Tropical Oscillation – A Review, Mon. Weather Rev., 122, 814–837, 1994. a
Marshall, A. G., Hendon, H. H., Son, S.-W., and Lim, Y.: Impact of the quasi-biennial oscillation on predictability of the Madden–Julian oscillation, Clim. Dynam., 49, 1365–1377, 2017. a, b, c
Mori, M. and Watanabe, M.: The Growth and Triggering Mechanisms of the PNA: A MJO-PNA Coherence, J. Meteorol. Soc. Jpn., 86, 213–236, 2008. a
Mundhenk, B. D., Barnes, E. A., Maloney, E. D., and Baggett, C. F.: Skillful empirical subseasonal prediction of landfalling atmospheric river activity using the Madden–Julian oscillation and quasi-biennial oscillation, NPJ Clim. Atmos. Sci., 1, 20177, https://doi.org/10.1038/s41612-017-0008-2, 2018. a, b, c
Nishimoto, E. and Yoden, S.: Influence of the Stratospheric Quasi-Biennial Oscillation on the Madden–Julian Oscillation during Austral Summer, J. Atmos. Sci., 74, 1105–1125, 2017. a, b, c, d, e, f, g
Pegion, K., Kirtman, B. P., Becker, E., Collins, D. C., LaJoie, E., Burgman, R., Bell, R., DelSole, T., Min, D., Zhu, Y., Li, W., Sinsky, E., Guan, H., Gottschalck, J., Metzger, E. J., Barton, N. P., Achuthavarier, D., Marshak, J., Koster, R. D., Lin, H., Gagnon, N., Bell, M., Tippett, M. K., Robertson, A. W., Sun, S., Benjamin, S. G., Green, B. W., Bleck, R., and Kim, H.: The Subseasonal Experiment (SubX): A Multimodel Subseasonal Prediction Experiment, B. Am. Meteorol. Soc., 100, 2043–2060, 2019. a
Richter, J. H., Deser, C., and Sun, L.: Effects of stratospheric variability on El Nino teleconnections, Environ. Res. Lett., 10, 12, https://doi.org/10.1088/1748-9326/10/12/124021, 2015. a
Sardeshmukh, P. D. and Hoskins, B. J.: The Generation of Global Rotational Flow by Steady Idealized Tropical Divergence, J. Atmos. Sci., 45, 1228–1251, 1988. a
Simpson, I. R., Blackburn, M., and Haigh, J. D.: The Role of Eddies in Driving the Tropospheric Response to Stratospheric Heating Perturbations, J. Atmos. Sci., 66, 1347–1365, 2009. a
Son, S.-W., Lim, Y., Yoo, C., Hendon, H. H., and Kim, J.: Stratospheric Control of the Madden–Julian Oscillation, J. Climate, 30, 1909–1922, 2017. a, b, c, d, e, f, g, h, i
Song, L. and Wu, R.: Modulation of the Westerly and Easterly Quasi-Biennial Oscillation Phases on the Connection between the Madden–Julian Oscillation and the Arctic Oscillation, Atmosphere, 11, 175, https://doi.org/10.3390/atmos11020175, 2020. a, b
Sun, L., Wang, H., and Liu, F.: Combined effect of the QBO and ENSO on the MJO, Atmos. Ocean. Sci. Lett., 12, 170–176, 2019. a
Sun, S., Bleck, R., Benjamin, S. G., Green, B. W., and Grell, G. A.: Subseasonal Forecasting with an Icosahedral, Vertically Quasi-Lagrangian Coupled Model. Part I: Model Overview and Evaluation of Systematic Errors, Mon. Weather Rev., 146, 1601–1617, 2018. a
Trenberth, K. E.: The Definition of El Niño, B. Am. Meteorol. Soc., 78, 2771–2777, 1997. a
Trenberth, K. and National Center for Atmospheric Research Staff (Eds.): The Climate Data Guide: Nino SST Indices (Nino 1+2, 3, 3.4, 4; ONI and TNI), available at: https://climatedataguide.ucar.edu/climate-data, last access: 24 April 2020. a, b
Tseng, K.-C., Barnes, E. A., and Maloney, E. D.: Prediction of the Midlatitude Response to Strong Madden-Julian Oscillation Events on S2S Time Scales: PREDICTION OF Z500 AT S2S TIME SCALES, Geophys. Res. Lett., 45, 463–470, 2018. a, b
Tseng, K.-C., Maloney, E., and Barnes, E.: The Consistency of MJO Teleconnection Patterns: An Explanation Using Linear Rossby Wave Theory, J. Climate, 32, 531–548, 2019. a
Vecchi, G. A.: The Madden-Julian Oscillation (MJO) and northern high latitude wintertime surface air temperatures, Geophys. Res. Lett., 31, 3500, https://doi.org/10.1029/2003GL018645, 2004. a
Vitart, F.: Madden-Julian Oscillation prediction and teleconnections in the S2S database: MJO Prediction and Teleconnections in the S2S Database, Q. J. Roy. Meteorol. Soc., 143, 2210–2220, 2017. a, b
Vitart, F., Ardilouze, C., Bonet, A., Brookshaw, A., Chen, M., Codorean, C., Déqué, M., et al.: The Subseasonal to Seasonal (S2S) Prediction Project Database, B. Am. Meteorol. Soc., 98, 163–173, 2017. a
Wang, J., Kim, H.-M., Chang, E. K. M., and Son, S.-W.: Modulation of the MJO and North Pacific Storm Track Relationship by the QBO, J. Geophys. Res.-Atmos., 123, 3976–3992, 2018. a, b, c, d
Wheeler, M. C. and Hendon, H. H.: An All-Season Real-Time Multivariate MJO Index: Development of an Index for Monitoring and Prediction, Mon. Weather Rev., 132, 1917–1932, 2004 (data available at: http://www.bom.gov.au/climate/mjo/graphics/rmm.74toRealtime.txt). a, b, c
Yoo, C. and Son, S.-W.: Modulation of the boreal wintertime Madden-Julian oscillation by the stratospheric quasi-biennial oscillation, Geophys. Res. Lett., 43, 1392–1398, https://doi.org/10.1002/2016GL067762, 2016. a, b, c
Zhang, C. and Zhang, B.: QBO-MJO Connection, J. Geophys. Res.-Atmos., 123, 2957–2967, 2018. a, b, c, d, e
Zheng, C., Kar-Man Chang, E., Kim, H.-M., Zhang, M., and Wang, W.: Impacts of the Madden–Julian Oscillation on Storm-Track Activity, Surface Air Temperature, and Precipitation over North America, J. Climate, 31, 6113–6134, https://doi.org/10.1175/JCLI-D-17-0534.1, 2018. a
Zhou, S., L'Heureux, M., Weaver, S., and Kumar, A.: A composite study of the MJO influence on the surface air temperature and precipitation over the Continental United States, Clim. Dynam., 38, 1459–1471, 2012. a
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(7419 KB) - Full-text XML
- Corrigendum
-
Supplement
(9019 KB) - BibTeX
- EndNote





